Defination - The Archimedean solids, consist of surfaces of more than a single kind of regular polygon, with identical vertices and identical arrangements of polygons around each polygon.In geometry, an Archimedean Solids is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices.
or as my class teacher told me that Archimedean solids are convex figures that can be made up of two or more types of regular polygons.All edge lengths of polygons are equal, and all vertices are identical. All vertices and angles are same.
or as my class teacher told me that Archimedean solids are convex figures that can be made up of two or more types of regular polygons.All edge lengths of polygons are equal, and all vertices are identical. All vertices and angles are same.
There are 13 Archimedean solids =
1) Truncated Tetrahedron=
The truncated tetrahedron is a Three Dimensional uniform polyhedron bounded by 4 hexagonal faces and 4 triangular faces. It is the simplest of the Archimedean polyhedra. It may be constructed by truncating the tetrahedron at 1/3 of its edge length.
The truncated tetrahedron has 18 edges, 6 of which correspond with the 6 edges of the tetrahedron. It has 12 vertices.
This is the diagram how to make a three dimensional Truncated Tetrahedron.
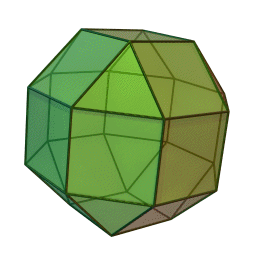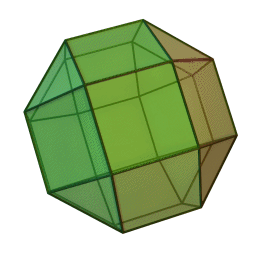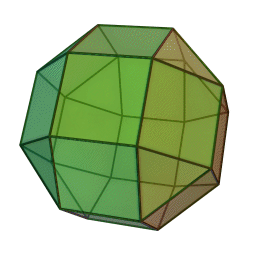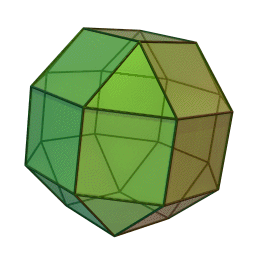
2) Cuboctahedron=
The cuboctahedron is a uniform polyhedron bounded by 6 squares and 8 triangles. It is edge-uniform, and its two kinds of faces alternate around each vertex, so it is also a quasi-regularpolyhedron. It may be constructed by truncating a cube or an octahedron at the midpoints of its edges (this process is known as rectification).
A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges.
This is the diagram how to make a three dimensional cuboctahedron.
3) Truncated Cube=
The truncated cube is a Three dimensional uniform polyhedron bounded by 8 triangles and 6 octagons. It may be constructed by truncating the cube's vertices at (2-√2) of its edge length. More simply, it may be constructed by radially expanding the cube's edges outwards by 1/√2 of its edge length and taking the convex hull. It may also be constructed by radially expanding the triangular faces of Cuboctahedron outwards.It has 36 edges, and 24 vertices.
4) Truncated Octahedron=
The truncated octahedron is a Three dimensional uniform polyhedron bounded by 8 hexagonal faces and 6 squares. It may be constructed by truncating the Octahedron at 1/3 of its edge length. It has 14 faces (8 regular Hexagonal and 6 Square), 36 edges, and 24 vertices.
This is how to make a Three dimensional model of Truncated octahedron.
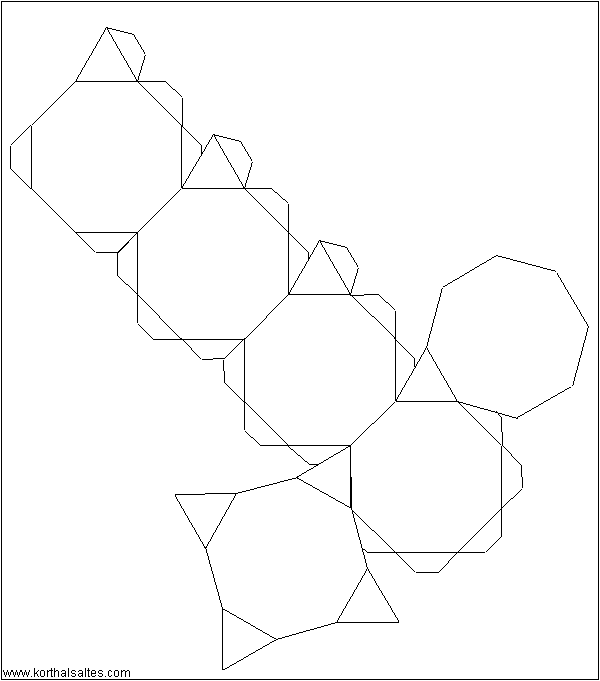
5) Rhombicuboctahedron=
The rhombicuboctahedron, also known as the small rhombicuboctahedron, is a three dimensional uniform polyhedron bounded by 8 triangles and 6+12=18 squares. It may be constructed by radially expanding the square faces of the cube outwards, or equivalently, radially expanding the triangular faces of octahedron outwards. There are 24 identical vertices, with one triangle and three squares meeting at each.
There are two distinct kinds of square faces on the rhombicuboctahedron: the first kind are the axial faces which are surrounded by 4 other square faces. There are six of these faces, and they correspond with the faces of a cube:
The second kind of square face are the non-axial faces, which are surrounded by 2 squares and 2 triangles. There are 12 of them, and they correspond with the edges of a cube:
It is important to distinguish between these two kinds of square faces, because their relative position to the triangular faces gives them different functions when the rhombicuboctahedron is fitted together with other polyhedra into 4D polytopes.
How to make a three dimensional rhombicuboctahedron.
The Truncated Cuboctahedron is a 3D uniform polyhedron bounded by 8 hexagons, 12 squares, and 6 octagons. It may be constructed by radially expanding the octagonal faces of the truncated cube outwards, or equivalently, radially expanding the hexagonal faces of the truncated octahedron, or the non-axial square faces of the rhombicuboctahedron.The great rhombicuboctahedron is also known as the truncated cuboctahedron; however, this is a misnomer. Truncating the cuboctahedron does not yield a uniform polyhedron, only a non-uniform topological equivalent of the great rhombicuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges.
This is how to make a three dimensional model of Truncated Cuboctahedron.
7) Snub cube=
The snub cube is a 3D uniform polyhedron bounded by 6 squares and 8+24=32 triangles. It is constructed by alternating the vertices of a suitably-proportioned, non-uniform great rhombicuboctahedron. It has 60 edges and 24 vertices.
The snub cube is chiral: its mirror image is distinct from itself. Its two forms are itsenantiomorphs, shown below:
The 32 triangular faces of the snub cube are of two kinds. The first kind, consisting of 8 triangles, corresponds with the vertices of the cube. These are shown below in yellow:
The remaining 24 triangular faces come in 12 pairs, corresponding with the 12 edges of the cube. The triangles in each pair share an edge with each other. These 24 faces are shown below:
This is how to make a three dimensional snub cube.
8)Icosidodecahedron=
The icosidodecahedron is a uniform polyhedron bounded by 12 pentagons and 20 triangles. It is edge-uniform, and its two kinds of faces alternate around each vertex, so it is also aquasi-regular polyhedron. It may be constructed by truncating the dodecahedron or the icosahedron at the midpoints of its edges.An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon.
This is how to make a three dimensional icosidodecahedron.
9) Truncated dodecahedron=
The truncated dodecahedron is a 3D uniform polyhedron bounded by 20 triangles and 12 decagons. It may be constructed by truncating the dodecahedron's vertices such that its pentagonal faces become decagons. Alternatively, it may be constructed by radially expanding the edges of the dodecahedron outwards, thus turning vertices into triangles and pentagons into decagons.It has 12 regular decagonal faces, 20 regulartriangular faces, 60 vertices and 90 edges.
This is how to make a three dimensional truncated dodecahedron.
10) Truncated Icosahedron=
The truncated icosahedron is a 3D uniform polyhedron bounded by 20 hexagonal faces and 12 pentagonal faces. It is one of the Archimedean polyhedra. It may be constructed by truncating the icosahedron at 1/3 of its edge length, and has 90 edges and 60 vertices.
The truncated icosahedron is widely recognized as the stitching pattern commonly used for soccer balls, and as the shape of the buckminsterfullerene molecule, C60. This latter association has given it the pet name buckyball.
This is how to make three dimensional truncated icosahedron.
11) Rhombicosidodecahedron/Small Rhombicosidodecahedron=
Rhombicosidodecahedron,also known as small rhombicosidodecahedron, is a 3D uniform polyhedron bounded by 20 triangles, 30 squares, and 12 pentagons. It may be constructed by radially expanding the pentagonal faces of the dodecahedron outwards, or equivalently, the triangular faces of the icosahedron outwards.
The 12 pentagonal faces correspond with the faces of the dodecahedron, the 20 triangular faces correspond with the faces of the icosahedron, and the 30 square faces correspond with the edges of both the dodecahedron and the icosahedron.
This is how to make a three dimensional Rhombicosidodecahedron
The great rhombicosidodecahedron is a 3D uniform polyhedron bounded by 20 hexagons, 30 squares, and 12 decagons. It may be constructed by radially expanding the decagonal faces of the truncated dodecahedron outwards, or equivalently, radially expanding the hexagonal faces of thetruncated icosahedron, or the square faces of the rhombicosidodecahedron. It has 120 vertices and 180 edges.
The great rhombicosidodecahedron is also known as the truncated icosidodecahedron; however, this name is a misnomer, because truncating the icosidodecahedron does not yield a uniform polyhedron, only a non-uniform topological equivalent of the great rhombicosidodecahedron. The correct derivation is as described above. Note also that there is a non-convex polyhedron known as the “great rhombicosidodecahedron”, which should not be confused with this convex polyhedron.
This is how to make a three dimensional Truncated Icosidodecahedron.
13) Snub Dodecahedron=
The snub dodecahedron is a 3D uniform polyhedron bounded by 12 pentagons and 20+60=80 triangles. It is constructed by alternating the vertices of a suitably-proportioned, non-uniform great rhombicosidodecahedron.
The snub dodecahedron, like the snub cube, is chiral: it is not the same as its mirror image. The following images show its two enantiomorphs (mirror images):
The 80 triangular faces of the snub dodecahedron are of two different kinds: the first kind shares all three edges only with other triangles, and the second kind shares an edge with a pentagon, another triangle of the second kind, and a triangle of the first kind. There are 20 triangles of the first kind, shown in cyan below:
This is how to make three dimensional snub dodecahedron.
No comments:
Post a Comment